It has been a while since the sunny spring day when I submitted my PhD thesis. As of last month, the thesis is no longer under embargo and publicly available from the University of Cambridge repository. Now seems like a good time to look back and remember the highlights, and what I learned as a researcher.

If you look near the start of the thesis, you will find an Abstract summarising the thesis in 340 words of dense technical language. Below, I attempt a more digestible explanation of my thesis, assuming no prior knowledge of turbomachinery. I discuss the background to the work first, followed by a summary of my key results.

Background

I was fortunate enough to be sponsored by Mitsubishi Heavy Industries for my doctoral research, meaning that my project was targeted towards their product: gas turbines for use in power stations. These burn natural gas, releasing stored energy and converting it into useful power. Basic thermodynamics shows that running a gas turbine hotter increases the efficiency of conversion, and hence reduces fuel consumption and carbon emissions. However, if the engine is too hot, then the metal parts will melt!

Gas turbines use film cooling to keep metal temperatures at a safe level. Film cooling works by making parts hollow, pumping cold air through them, and then ejecting the cold air through holes in the surface. This forms a protective layer between the metal and hot combustion gases:

*Figure: The basic concept of film cooling. Cold air is ejected from a hollow surface and forms a protective film that shields the metal from hot air.*

The concept is simple, but the implementation can be quite elaborate with many internal passages and external holes:

Figure: Cooling system of a turbine blade, adapted from Han (2003), CC BY 3.0.

Designing film cooling systems is not straightforward. The inside of a gas turbine is a harsh environment, with a temperature four times hotter than a domestic oven. The lifespan of metal components is very sensitive to their temperature, so the cooling system has to be reliable. Engineers do not have accurate tools for predicting temperatures in the engine, so designers rely on rules of thumb, past experience and a generous safety margin. We don’t know if a proposed design will actually work until it is built and tested at great expense, so it is important to get it right the first time round.

Current tools for predicting temperatures in the engine make certain simplifying assumptions, which are not strictly true but make the prediction easier to calculate. One such assumption is the neglect of blade row interactions. The gas turbine is made of alternating stationary and rotating rows of blades, which are turned by air flow to extract power, a bit like a windmill. The condition of the air will change over time as rotating blades move past stationary blades. This is best illustrated with some animations of the air within a gas turbine:

*Figure: Blade row interactions in a turbine stage. The left-hand row of blades shed 'wakes' behind them, which move downstream and flow through the right-hand row.*

Behind each of the left-hand blades is a dark coloured region of low-velocity air, caused by friction against the surface of the blade. These are called ‘wakes’, by analogy with the disturbed water behind a boat. The wakes are carried downstream and through the right-hand row of blades.

A cooling hole situated in the right-hand row experiences a time-varying air flow as each wake comes past. However, the existing design tools available to an Engineer neglect this effect, and instead assume the flow is steady, like this:

*Figure: Time-averaged flow field in a turbine stage.*

My thesis set out to examine the validity of the steady flow assumption, and quantify the error associated with neglecting unsteady blade row interactions when designing film cooling.

Key results

Low-fidelity computations

I used low-fidelity computations, not including coolant films, to identify the physical causes of blade row interaction. The results look something like the animation above, and I concluded that the wakes were the most important factor. I used further results from these simulations to show that the flow rate through cooling holes varies by at least 30% as a wake passes by.

Experimental

I designed and built a new apparatus to test the performance of film cooling holes subject to time-varying flow conditions. This was a single row of cooling holes on a flat surface, modelling a small part of the real gas turbine.

The measurements I took showed that unsteadiness is important when the response of a cooling hole to changes in flow rate is non-linear. This rather technical word means that the temperature always goes down if the flow rate changes away from a certain value. The opposite is linear: temperature goes down as flow rate goes up, and vice versa. If we plot temperature against flow rate on a graph, the linear and non-linear regions look like this:

Figure: Linear and non-linear behaviour of a film cooling hole.

An Engineer should pick a flow rate in the linear region of the graph, so that blade row interactions do not affect the film cooling.

High-fidelity computations

The previous computations did not include the coolant film, and hence could not provide temperature predictions. I developed a higher-fidelity computational approach that includes the coolant film to quantify the impact of unsteadiness on temperatures in a real turbine, as opposed to my simplified experiment. This is difficult because the flow in the coolant films is complex and intricate — I needed to use 32 computers continuously for two months to complete the simulation! The results showed that blade row interactions had different effects on each side of the rotor blades.

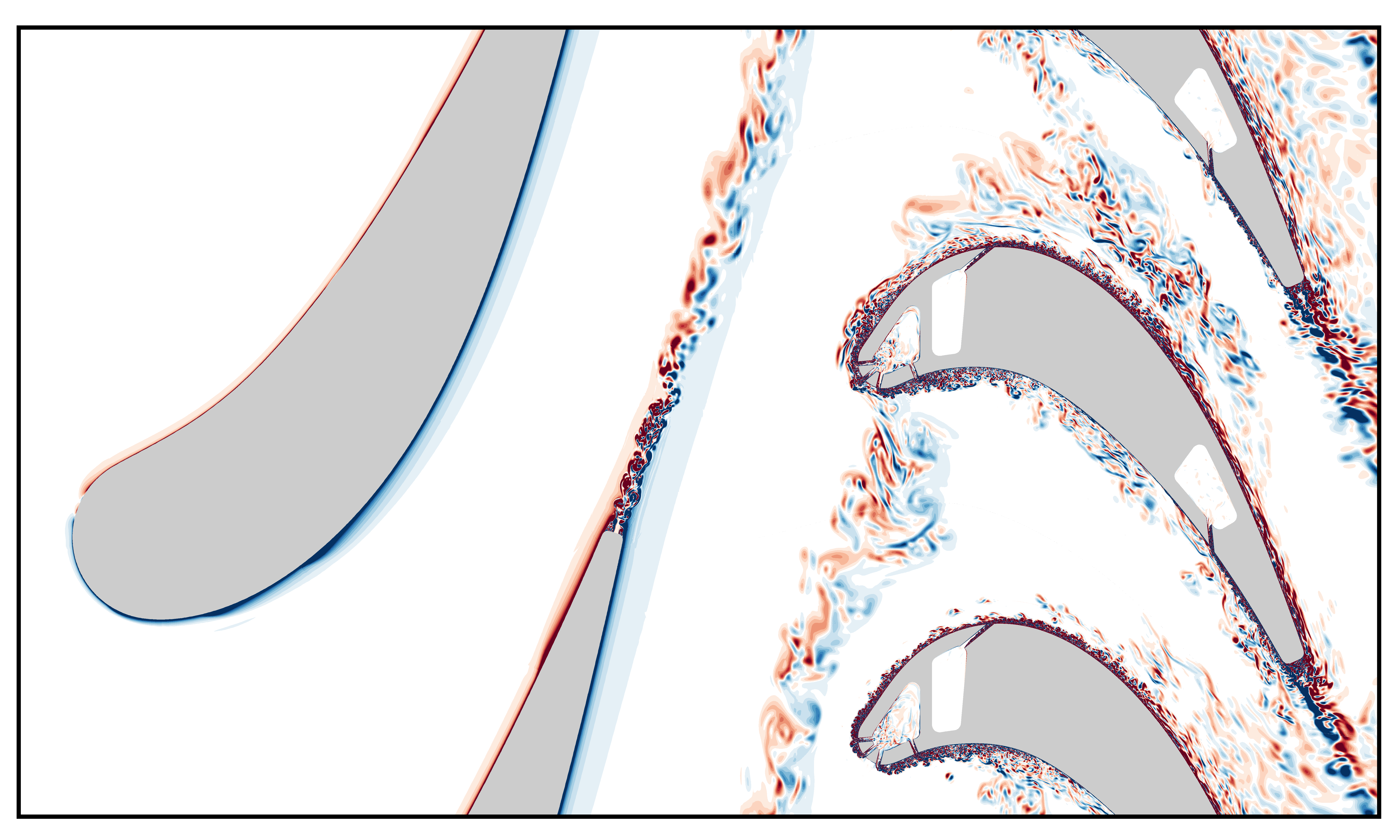Figure: My simulation of the intricate flow structures in a cooled turbine blade.

Conclusion

I have presented a lay-person’s summary of the key results from my PhD research, and there is a lot more detail in the thesis. Almost as important to me, but not written down anywhere, is the knowledge I personally gained during the process. I was able to do a whole range of interesting things: build new experiments, run big computations, and derive my own mathematical models. Fortunately, the culture of the Whittle Laboratory is that people help each other, and I learned a great deal about how to do research from my colleagues along the way.